Canibekov təsiri

Bu gün maraq göstərənlər üçün fizika sahəsindən bir şey: Canibekov təsiriTenis raketi teoremi olaraq da bilinən, üç fərqli ətalət anı ilə fırlanan cisimlərin qeyri-sabitliyini izah edir. Atalet momenti, cismin fırlanma hərəkətindəki dəyişikliklərə müqavimətini göstərir. Xüsusi fırlanma oxundan və həndəsədən asılıdır. Klassik Hamilton sistemlərinin dinamikasını başa düşmək, riyazi təsvirlərindən dəfələrlə çox sayda tətbiqetmə ilə hələlik həlledici bir hədəfdir. Bir neçə azadlıq dərəcəsi olan inteqrasiya edilə bilən sistemlər halında, səmərəli bir yanaşma mexaniki sistemin dinamik xüsusiyyətlərini xarakterizə etmək üçün həndəsi bir təhlilə əsaslanır. Bu cür həndəsi fenomenlər bir qayda olaraq təcrübə yolu ilə müşahidə edilə bilən müəyyən effektlərin möhkəmliyinin mənşəyidir. bunlardan biri sözdədir. Canibekov təsiri ya da tennis raket effekti adlanır.

BSS-nin çəkisizliyində Canibekov təsiri

Fenomenin mükəmməl və detallı bir nəzəri çıxışı burada tapıla bilər (https://arxiv.org/pdf/1606.08237.pdf). Biz burada bir az daha kobud, lakin buna baxmayaraq fenomeni izah edən biri ilə işləyirik. Təəssüf ki, sərt cisimlərin dinamikası haqqında əvvəlcədən biliklərin olması lazımdır:

I1 və I2 və I3 ətalət məqamları ilə ətalət matrisini (diaqonallaşdırılmış) nəzərdən keçirək ki, I1 ən kiçik, I3 isə ən böyük olsun. İndi əsas ətalət momentinin oxu I3 ətrafında olan hərəkəti nəzərdən keçirin. Açısal sürət vektoru:

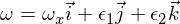
epsilonların digər iki əsas oxdakı kiçik narahatlıqlar olduğu yer. İndi bunu Eyler tənliklərinə daxil etsəniz, aşağıdakıları əldə edəcəksiniz:

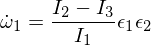
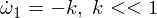
İndi ikinci Eyler tənliyini fərqləndiririk:

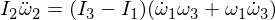
İfadəmizdəki omeqa 1 və omega 3-un əvəzlənməsi və epsilonların çoxaldılması onları görməməzlikdən gələni etdiyindən,

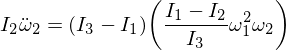
Bu, bizə Omega 2 formasının diferensial tənliyini verir:

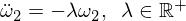
Əsas həll yolu:

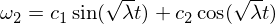
Bu səbəbdən omeqa-1 oxundakı fırlanma pozğunluğunun sabit olduğunu və periyodik hərəkətlər etdiyini və ya sərt bədən hərəkəti terminologiyasında bir presessiya etdiyini bilirik. Omeqa 3 pozğunluğu yuxarıda göstərilənlərə bənzər bir mübahisəni izləyir və bunu həll etməyiniz üçün bir məşq olaraq buraxacağam. Aralıq ox üçün bizdə var:

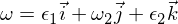
Eyler tənliklərinə daxil edilmişdir:

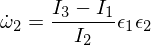
Üçüncü Eyler tənliyini fərqləndirmək aşağıdakıları verir:

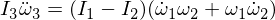
Gəlin ifadələrimizi əvəz edək:

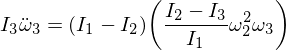
İndi yenidən qurun və aşağıdakı diferensial tənliyi çıxarın:

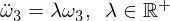
Diqqət yetirin ki, katsayının indi pozitiv olduğu, bu səbəbdən də eksponent həllərə səbəb olduğu:

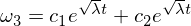
Bu həll omeqa 3-ün omeqa 2-nin pozulması ilə ara ox boyunca qeyri-sabit olduğunu göstərir!

Bu nə deməkdir?

İndi əldə etdiyimiz və teoremi anlamağı öyrəndiyimiz hər şeyi birləşdirə bilərik. Sadə dillə desək, ara ox boyunca fırlanma pozulursa, eksponent həllər ilə diferensial tənlik yaranır. Bu, digər iki oxda müşahidə olunan dəqiq hərəkətdən fərqli olaraq qeyri-sabit bir hərəkətə gətirib çıxarır. Bu nəticə olduqca təəccüblüdür. Aralıq ətalət anının niyə qeyri-sabit bir dönmə ilə nəticələnəcəyini təsəvvür edə bilmədiyimiz üçün belə bir teorema üçün intuitiv bir dəstək yoxdur. Göründüyü kimi tamamilə riyazi xarakter daşıyır.